Стълбове, допирателната кръгове
Ако искате да изпробвате силата си и да видим резултата като сте готови за изпита или OGE?
1. Определения и основната теорема
В обикновения живот, вие сте много добре запознати с това, което думата "докосване". И представете си, в областта на математиката, също има такова нещо. В този брой ще разгледаме, за да изразите "направо до кръга" и "два кръга докосване."

Директно до кръга, ако има точно една обща точка.
Тази линия се нарича допирателна към този кръг.
Погледнете внимателно: много прилича на живота, нали? Директно на снимката само леко докосва кръга се докосне.
Е, и по същия начин:

Две кръгове са свързани, ако те имат точно една обща точка.
Какво трябва да знаете за тангенти и до кръга?
Най-важната теорема гласи, че:

Radius, прекарано в точката на докосване, перпендикулярна на допирателната.
Не забравяйте, че точно като таблицата за умножение! Всички други факти за допирателните и до кръга, се основава на тази теорема.
За да го докаже, ние няма да (можете да погледнете в следните нива на теория), но тъй като това е най-важните творби на теоремата, вижте сега няколко пъти.
2. Ъгълът между допирателната и акорда

Ъгълът между допирателната и акорда е равна на половин градус мярка дъга, която е вътре в ъгъла.

Тук можем само да си припомни, че в дъгата на един и същ номер на степените по централния ъгъл можем да заключим, че има dugu.To "градусова дъга мярка" - е "колко градуса в центъра на ъгъл" - и всички!
Е, Карлсон казва: "продължите разговора".
Начертайте отново теоремата на ъгъла между допирателната и акорд.

Погледнете акорд счупи кръга на две дъги. Една дъга е на ъгъла. и другата дъга - в ъгъл.
И ъгъл теорема между допирателната и каза, акорд, който е равен на половината от ъгъла. Половина е по-голяма (на фигурата - зелен) ъгъл.
Какво е това, че радиуса, за да точката на докосване, перпендикулярна на допирателната?
Сега и ние виждаме. - радиусът, - допирателна.

Средства. Ето защо. Но (и - радиус).
И остава да се напомни, че ъглите на триъгълник е равен на сбора.

Това е страхотно, нали? И най-важното нещо е, че.
3. уравнението на допирателната линия сегменти дължината на допирателната
"И колко тангенти може да се извършва от една точка до един и същи кръг," Мислили ли сте за този въпрос? Сега, представете си, точно две! Ето как:

И още по-изненадващо, факт е, че:
Простира тангента, съставен от една точка до окръжност равен.
Това означава, че в нашата рисунка.
И този факт, също най-важното нещо е, че радиусът, проведено от точката на докосване, перпендикулярна на допирателната.
Ето, уверете се, че: прекарват радиуси и и и да се свържете.
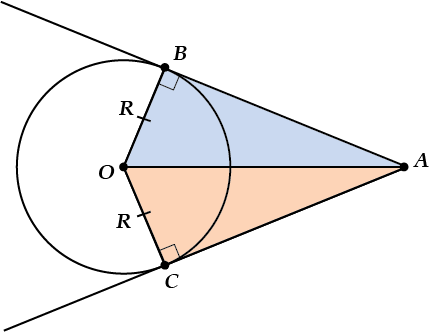
радиус.
- Tangent, искам да кажа.
Е, по същия начин.
Има две правоъгълни триъгълници и. в която:
(Виж в темата "правоъгълен триъгълник", ако не си спомняте, когато има правоъгълни триъгълници).

И пак повтарям - това е един много важен факт:
Сегменти на тангенти, съставени от една единствена точка - равен.
А има и друг факт, който ние не трябва да се докаже, но тя може да бъде полезна за вас при решаване на проблеми.

За всяка линия. пресичащи се кръгове, където - дължината на допирателната.
Умни думи говорят за това по този начин:
"Пл сегмент на дължина, равна на произведението от тангенса пресичащи на външната част."
Страшен? Не се страхувайте, просто не забравяйте, че това е в буквите:

4. обща допирателна към две окръжности

Линията, която докосва два кръга, се нарича общата им допирателна.
Общи допирателни са външни и вътрешни.
Погледнете снимките.
Декларация за поверителност
Защитете личните си данни е важно за нас. Поради тази причина, ние сме разработили Декларация за поверителност, която се описва как се използва и съхранява информацията си. Моля, прегледайте нашата спазване на правилата за поверителност и да споделите с нас, ако имате някакви въпроси.
Събиране и използване на лична информация
В рамките на личната информация се отнася за данни, които могат да се използват за идентифициране на конкретен човек или комуникация с него.
От вас може да бъде поискано да предостави личната Ви информация по всяко време, когато общувате с нас.
Следват няколко примера за видовете лична информация, която може да събира, и как можем да използваме тази информация.
Каква лична информация събираме:
Как да използваме вашата лична информация:
- Ние събираме лична информация ни позволява да се свържем с вас и да информира за уникални оферти, промоции и други събития и предстоящи събития.
- От време на време, ние може да използваме вашата лична информация, за да изпратите важни известия и съобщения.
- Ние можем да използваме лична информация за вътрешни цели, като например одит, анализ на данни и различни изследвания, за да подобрим нашите услуги и ще ви даде съвети за нашите услуги.
- Ако участвате в томбола, конкурс или други подобни, позволяващи дейности, ние може да използваме информацията за управлението на такива програми, които предлагате.
Разкриване на информация на трети страни
Ние не разкрива информация, получена от вас на трети лица.
- Ако трябва да - в съответствие със закона, съдебна заповед, в процеса, и / или въз основа на обществени запитвания или искания от публични органи на територията на България - да разкрием вашите лични данни. Възможно е да разкрием информация за вас, ако преценим, че това разкриване е необходимо или подходящо за целите на сигурността, прилагането на закона или други обществено значими дела.
- В случай на реорганизация, сливане или продажба ние може да прехвърли на лична информация, която събираме, подходяща трета страна - на правоприемника.
Защита на личната информация
Ние сме като предпазни мерки - включително административни, технически и физически - да се защити вашата лична информация срещу загуба, кражба и злоупотреба, както и срещу неоторизиран достъп, разкриване, промяна или унищожаване.
Защитавайте поверителността на фирмено ниво
С цел да се гарантира, че вашата лична информация е защитена, ние носим стандарти за конфиденциалност и сигурност на нашите служители, както и стриктно да следи за изпълнението на мерките за конфиденциалност.