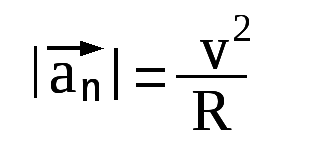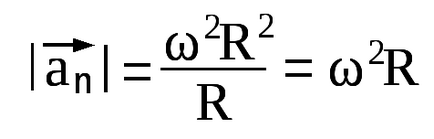Кинематика на въртеливо движение
ъглова скорост вектор на ъгъла на въртене, ъгловото ускорение
Съобщение линейна и ъглова скорост
Съобщение линейни и ъглови характеристики
1. тангенциална и нормалното ускорение
Две компоненти ускорение: тангенциален ускорение и нормално ускорение.
Тангенциална ускорение е насочено по допирателната към траекторията
Нормално ускорение е насочено по нормалата към траекторията
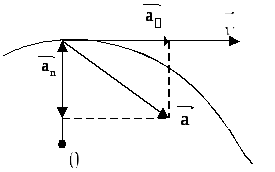
Тангенциално ускорение характеризира със скоростта на промяна в стойността. Ако скоростта не се различават по големина, тангенциалната съставна е равна на нула, а нормалната компонента на ускорението е пълно ускорение.
Нормално ускорение характеризира със скоростта на промяна на посоката. Ако посоката на скоростта не се променя, се появява движението по праволинейна траектория.
Като цяло, общото ускорение:
По този начин, нормален компонент на вектора на ускорение
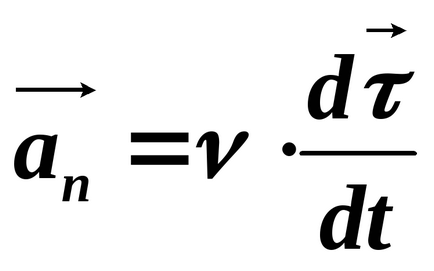
За да разберете свойствата на нормалното ускорение, е необходимо да се установи това, което определя
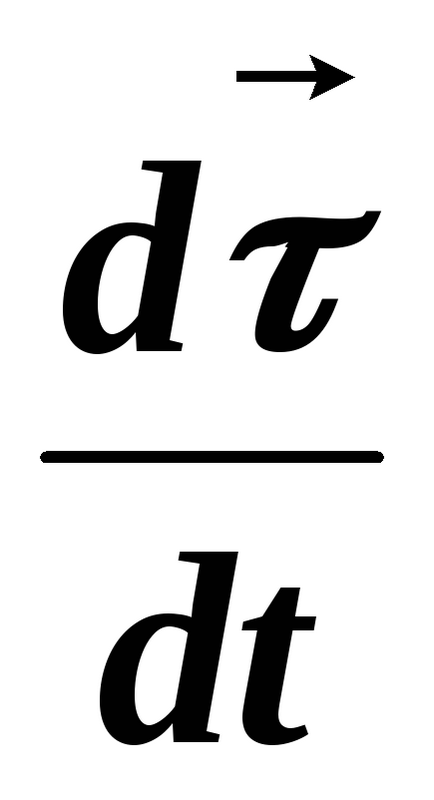
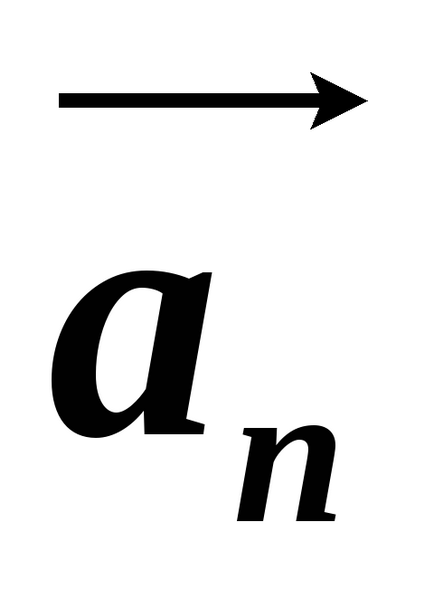
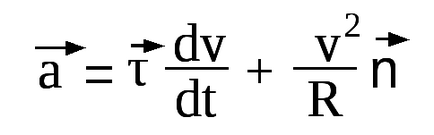
2. Радиусът на кривината на траекторията
Радиусът на кривината - радиус на окръжността, която се слива в това място с безкрайно част на кривата.
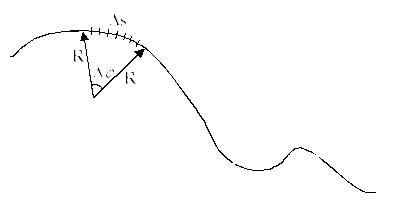
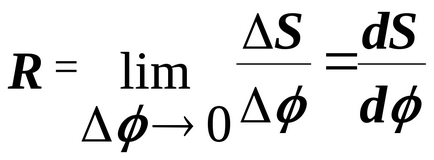
3. ъглова скорост вектор на ъгъла на въртене, ъгловото ускорение.
Всяко въртене е напълно определена чрез определяне на оста на въртене и ъгълът povorotaΔφotnositelno тази ос. Ако въртенето се извършва на малък ugolΔφ <<2π, то можно ввести понятие вектор угла поворота.
вектор
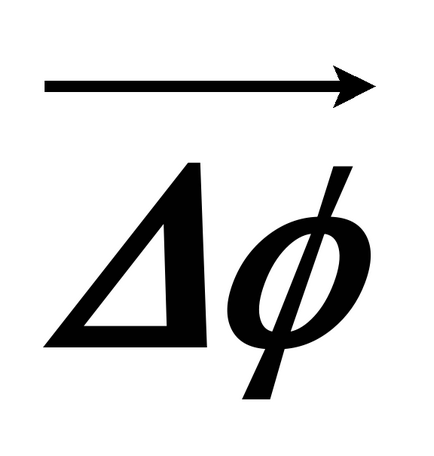
Ориентацията на този вектор се определя от принципите на дясната страна.
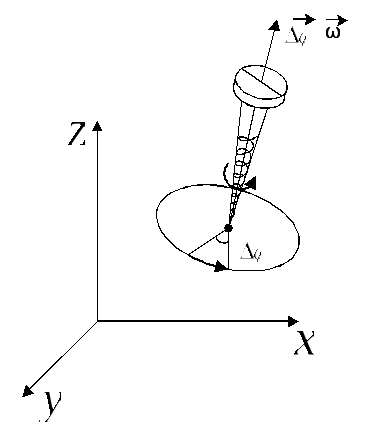
Абсолютната стойност на вектора
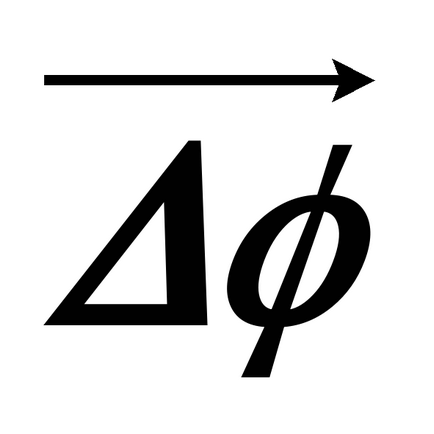
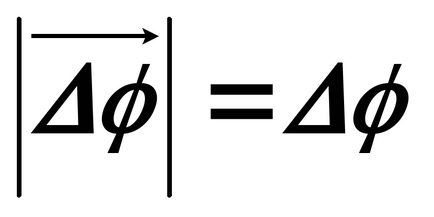
За да определите стойността вектор е, тя трябва не само посоката и абсолютната стойност, но и да отговаря на правилото на допълнение вектор. Може да бъде показано, че добавянето вектор на два ъгъла на въртене на успоредник не се извършва. Тя ще бъде валидна само за malogoΔφ <<2π
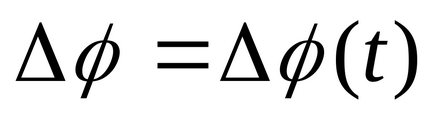
Ъглова скорост е вектор
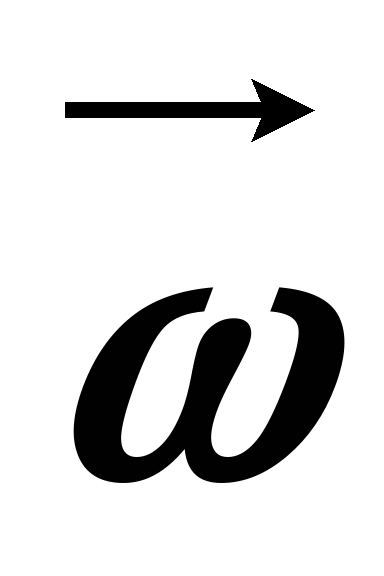
дължина на вектор
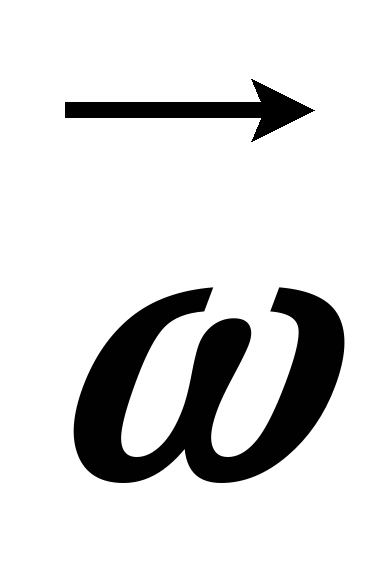
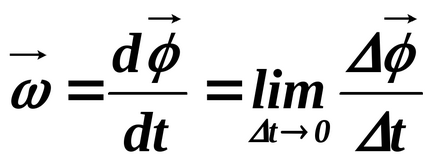
Ъглова скорост, за разлика от ъгъла на завъртане, пълен вектор.
вектор
Промяната с време на ъгловата скорост се характеризира с ъгловото ускорение:
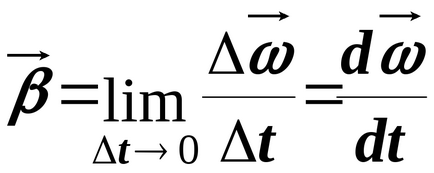
ъглов модул ускорение се измерва в
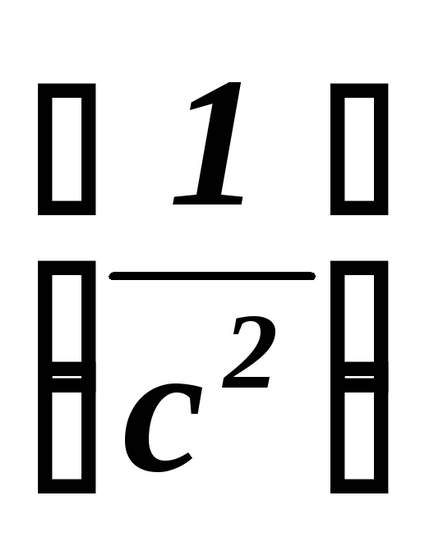
Ъгловото ускорение както и ъгловата скорост - псевдо.
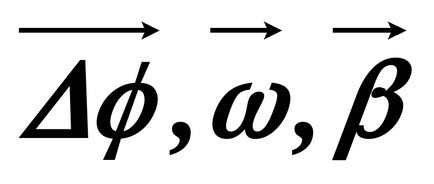
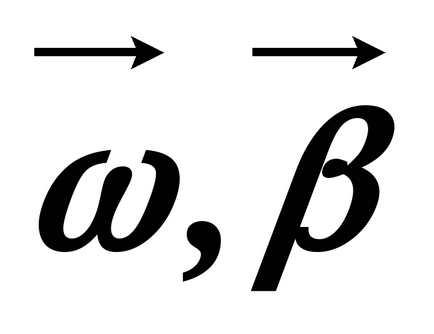
4. Комуникация линейна и ъглова скорост
Нека за malyyΔttelo обърна naΔφ. Нека точките от
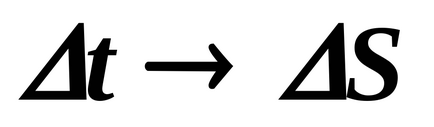
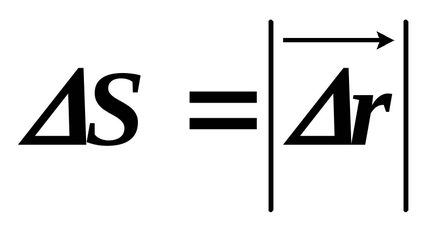
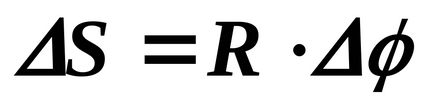
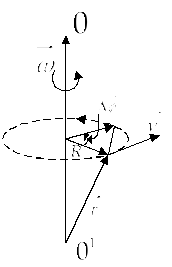
линеен модул скорост
Съобщение векторите на линейни и ъглови скорости: позицията на точка се определя от вектора на радиус

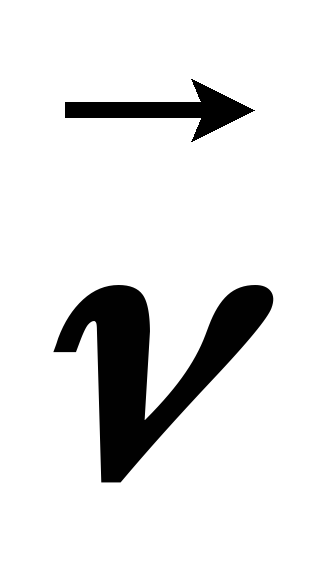
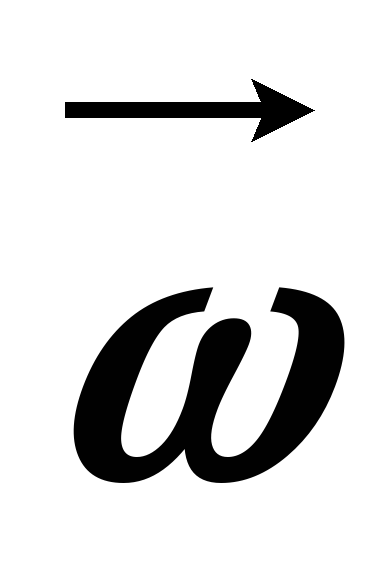

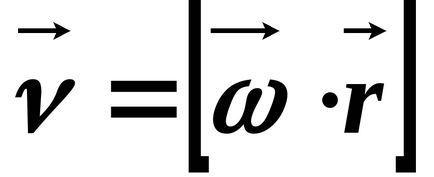
Промяната на вектора на радиус

5. Комуникационни линейни и ъглови характеристики