Повърхността на цилиндъра - с формула, пример за изчисление

Цилиндърът е геометрично тяло, ограничена от две успоредни равнини и с цилиндрична повърхност.

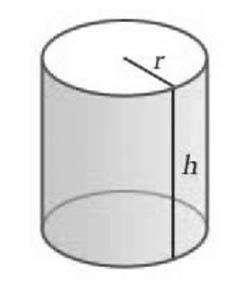
Цилиндърът включва странична повърхност и две основи. Формула площ на повърхността на цилиндър включва отделна изчисляване на квадратна основа и страничната повърхност. Тъй като основата на цилиндъра са равни, тогава общата площ ще се изчислява съгласно формулата:

Пример за изчисляване на площта цилиндър ние ще се грижат научите всички необходими формули. За да започнете, ние се нуждаем от формула поле на основата цилиндър. Тъй като в основата на цилиндър е кръг, ние трябва да се приложи формула областта на кръг.
Ние се помни, че в тези изчисления използването на постоянен брой π = 3,1415926, който се изчислява като съотношението на обиколката на нейния диаметър. Този номер е математическа константа. Пример за изчисляване на цилиндър базовата площ, ние също ще разгледаме малко по-късно.

Площта на повърхността на бутилката

Формула площ на страничната повърхност на цилиндъра е продукт на дължината в основата си височина:

А сега да разгледаме проблема, в който ние трябва да се изчисли общата площ на цилиндъра. На Фигура предварително определена височина Н = 4 см, R = 2 см. Откриваме пълно областта на цилиндъра.
За да започнете да се изчисли база площ:
А сега да разгледаме примера на зоната за изчисляване на страничната повърхност на цилиндъра. В разпънат вид, той е правоъгълник. Площта се изчислява съгласно горната формула. Заместник в нея всички данни:
Брутна площ на окръжност е сумата от базовата площ и двойно страна:

По този начин, като се използва формула областта на базите и страничните повърхностни форми, ние може да намери общата повърхност на цилиндъра.
Аксиална част на цилиндъра е правоъгълник, в който двете страни са равни височина и диаметър на цилиндъра.

Формула аксиално сечение на цилиндъра се получава от формулата за изчисляване на областта на правоъгълник:

Вземем примера на изчисляване на площта на аксиално сечение на цилиндъра. За това ние приемаме условията на проблема бе споменато по-горе. За да разберете стойността имаме нужда диаметър. Ние знаем, че тя е равна на два пъти радиуса:

Заместник на данните: