ъгъл тригонометрия - ъгъла на завъртане

В тригонометрията важно понятие е на ъгъла на завъртане. По-долу ние постоянно ще осигури оглед на търна и въведете всички свързани с понятията. Да започнем с една обща представа за струговане, казват за един пълен оборот. Следваща пристъпи към концепцията на ъгъла на въртене и разглежда неговите характеристики като посоката и количеството на въртене. И накрая, ние определяме фигурата въртене около точка. Цялата теория на текста ще предоставя примери и обяснителни графични илюстрации.

Навигация в страниците.

Какво се нарича повратна точка по точка?

Сега, ние се отбележи, че, заедно с фразата "обърнеш точка" ще използва фразата "до около точка" и "точка на въртене роднина", което означава едно и също нещо.

Ние въвеждане на концепцията за повратна точка по точка.

Първо ние определяме центъра на въртене.

Въпросът за който се извършва ротация, се нарича център на въртене.

Сега нека да кажем, че е в резултат на повратна точка.

В резултат на въртенето на точка А по отношение на точка O на въртене център се получава А1 (което в случай на множество завъртания може да съвпада с А), където А1 е разположен на окръжност с център в радиус О ОА. С други думи, когато се върти около точката O движи точка А до точка А1. лежи на окръжност с център в точка радиус О ОА.

Смята се, че в точката О се върти около себе си продължава по себе си. Това означава, че чрез въртене около точката на въртене център О О преминава в себе си.

Заслужава да се отбележи също така, че е на въртене точка А към точка О се счита за движение от движението на точка А по периферията с центъра в точка радиус О ОА.

За яснота, илюстрация на точката на въртене около една точка О. А на фигурата по-долу, изместване на точка А до точка А1 показват чрез стрелки.

пълен оборот

Човек може да се извърши като точка на въртене А спрямо центъра на въртене О. А. преминаване че точка всички точки на кръга, ще бъде на едно и също място. В същото време се казва, че точка А е направила пълен оборот около точката О.

Нека се даде нагледна илюстрация на общия оборот.

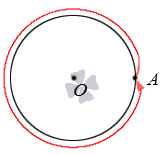
Ако нямате спре на една революция, и да продължи да се движи точка на кръга, това е възможно да се извърши две, три и така нататък пълна скорост. На фигурата в долния десен ъгъл показва как две пълни обороти, а в ляво може да се произвежда - три завои.

Можете също така да се говори за частите на пълен оборот, например, около половината от оборота, трети, четвърти и т.н. завъртете (ако е необходимо, вижте статията и да споделят общи части).

Концепцията на ъгъла на завъртане

От въведен в първия параграф на концепции се върти точка е ясно, че има безкрайно много варианти на А въртене около точка О. В действителност, всяка точка на окръжността с център в радиус от точка O ОА може да се разглеждат като точка А1. получената точка на въртене А. Следователно, за да се разграничат една от друга страна, въвежда концепцията на ъгъла на въртене.

Една характеристика на ъгъла на въртене е посоката на въртене. В посоката на въртене се съди за това как да прилагат точка на въртене - по часовниковата стрелка или обратно на часовниковата стрелка.

Друга характеристика на въртене ъгъл е стойността си. ъглите на въртене се измерва в същите единици като ъглите в геометрията. най-често срещаните степени и радиани. Тук следва да се отбележи, че ъгълът на въртене в градуси може да се изрази по всяко реално число в интервала от минус безкрайност до плюс безкрайност, за разлика от ъгъл геометрия, чиято стойност е положителна в градуси и не надвишава 180.

За да посочите, ъгли на въртене обикновено се използват малки букви от гръцката азбука и т.н. с една буква индекси често се използват за обозначаване на голям брой ъгли на въртене, например.

Сега нека да поговорим за характеристиките на ъгъла на завъртане и още в ред.

Посоката на въртене

Нека окръжност с център в точка О маркираната точка А и А1. точка А1 може да се стигне от точка А да се върти около центъра на О или по часовниковата стрелка или - обратно на часовниковата стрелка. Тези обрати логически да мислят различно.

Договорена да се помисли за въртене в положителна посока на завой, който се извършва обратна на часовниковата стрелка. Завъртането се нарича въртене в отрицателна посока.

Илюстрира ротации в положителни и отрицателни посоки. Фигурата по-долу показва, ляв завой в положителна посока, както и правото - отрицателно.

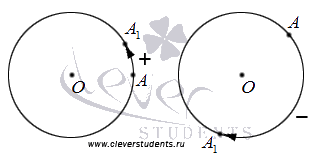
Големината на ъгъла на завъртане, ъгълът на произволна величина

Corner точка на въртене различен от центъра на въртене, е напълно определя от посочване на стойността му, от друга страна, степента на ъгъла на завъртане може да се съди за това как е било извършено тази промяна.

Както споменахме по-горе, големината на ъгъла на завъртане в градуси, изразена като броя на -∞ до + ∞. Тук знака плюс съответства на въртене по посока на часовниковата стрелка, както и знак минус - завъртете обратно на часовниковата стрелка.

Сега ние трябва да се установи съответствие между размера на ъгъла на завиване и така някои свой ред тя отговаря.

Започваме с ъгъл на завъртане на нула градуса. Този ъгъл на въртене съответства на изместване от точка А към себе си. С други думи, когато се върти около 0 градуса точка O точка А остава на мястото си.

Продължете да се обърнеш точка О. момент, в който се осъществява въртене в рамките на половин оборот. Ние приемаме, че точка А се премества в точка А1. В този случай, абсолютната стойност на ъгъла в градуси не AOA1 надхвърля 180. Ако въртенето е в положителна посока, стойността на ъгъла на завъртане се счита за равно на AOA1 на ъгъл. и ако въртенето е в отрицателна посока, след това си стойност се счита за равна на AOA1 ъгъл отрицателен. Например нека илюстрация, показваща въртене ъгли на 30 180 и -150 градуса.

Ъгъла на въртене по-голяма от 180 градуса и по-малко от -180 градуса определят въз основа на следните свойства доста очевидни последователни завои. няколко последователни завъртания около център точка А О еквивалент на един оборот на, степента на което е равно на сумата от стойностите на тези завои.

Ето един пример, който илюстрира този имот. За да се върти по отношение на точка А точка О от 45 градуса, а след това този момент все още се върти 60 градуса и след това се върти тази точка от -35 градуса. Ние означаваме тези междинни точки на двете ъгли А1. А2 и А3. В същата тази точка A3 бихме могли да получите, като следвате една точка на въртене А под ъгъл от 45 + 60 + (- 35) = 70 градуса.

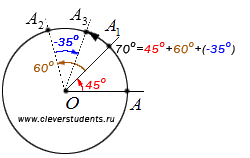
По този начин ъглите на въртене, по-голям от 180 градуса, ние ще представят няколко последователни намотки в ъглите, което дава сумата от стойността на първоначалния ъгъл на въртене. Например, ъгълът на завъртане на 279 градуса съответства последователни завъртания на 99 и 180 градуса, или 90 и 90. 90. 9 градуса, или 180 до 180 и -81 градуса, или 279 последователни намотки на 1 градус.

По същия начин се определя и въртене ъгли по-малко от -180 градуса. Например, ъгълът на въртене на -520 градуса може да се тълкува като повратна точка последователно -180. -180 и -160 градуса.

За да обобщим. Ние определено от ъгъла на завъртане, чиято стойност се изразява в градуси някои реално число в интервала от -∞ до + ∞. В тригонометрията, ние ще работим конкретно с ъгли на въртене, въпреки че думата "завой" често се пропуска, а просто да каже "ъгъл". По този начин, в тригонометрията, ние ще работим с произволно големи ъгли, с която имаме предвид ъгли на въртене.

В заключение този раздел, ние се отбележи, че пълен ред съответства на ъгъла на завъртане на 360 градуса в положителна посока (или 2 · пи радиана), и в отрицателната - ъгъла на завъртане при -360 градуса (или -2 · π RAD). Удобно е да представлява по-големи ъгли на въртене и на определен брой пълни обороти и друг завъртане на стойност под ъгъл от -180 до 180 градуса. Помислете например за ъгъла на въртене 1340 градуса. Лесно 1340 представени като 4 · 360 + (- 100). Това означава, че първоначално ъгъла на завъртане съответства на 4 пълни оборота в положителна посока и последващото търна до -100 градуса. Друг пример -745 градуса ъгъл на завъртане може да се тълкува като две завъртания на часовниковата стрелка и последващо завъртане от -25 градуса, като -745 = (- 360) + 2 · (- 25).

фигура въртене около точка ъгъл

Понятието точка на въртене може лесно да бъде разширена, за да се върти около всяка цифра от ъгъла на точка (това е за такова въртене като точката за която се извършва въртенето, и на фигурата, който се завърта, за да лежат в една равнина).

Чрез завъртане на фигурите означава цялата форма завой точки около предварително определена точка под определен ъгъл.

Като пример, графичен следния: изпълни своя сегмент AB под ъгъл спрямо точката О. Този сегмент при включване ход в А1 В1 сегмент.